NONLINEAR CONJUGATE GRADIENTS FOR SCALING SYNCHRONOUS DISTRIBUTED DNN TRAININGについてまとめた

「NONLINEAR CONJUGATE GRADIENTS FOR SCALING SYNCHRONOUS DISTRIBUTED DNN TRAINING」の論文をまとめました

論文pdf：https://arxiv.org/pdf/1812.02886.pdf

落合フォーマット(http://lafrenze.hatenablog.com/entry/2015/08/04/120205)でまとめました。

どんなもの？

ここではDeep neural networkのoptimizerとしてstochastic preconditioned nonlinear conjugate gradientのアルゴリズムを提案・評価をしています。

つまり非線形共役勾配法をoptimizerとして応用してみたといった感じです。

非線形共役勾配法については

http://www.orsj.or.jp/archive2/or59-03/or59_3_131.pdf

http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1362-13.pdf

を見れば分かりやすいと思います。

ちなみに論文によると

We hypothesize that with large mini-batches, the variance of the gradients is reduced, which makes NLCG method effective for DNN training.（大規模なミニバッチでは勾配の分散が減少し、それが非線形共役勾配法を深層学習に適用できると仮定した。

とあるように大規模なミニバッチに注目しています。

先行研究と比べてどこがすごい？

近年Deep Neural Network （DNN）学習では、未だにoptimizerのアルゴリズムとしてStochastic Gradient Descent (SGD)などが主流として使われています。

SGDなどよりも大きなミニバッチサイズを使用できる効率的なアルゴリズムだと主張しています。

～ 補足 ～ ※SGDの他にMomentum SGD、RMSProp、 Adam (Kingma & Ba, 2014),、ADAGradなどの1次微分を用いた最適化手法があります。 共役勾配法を使うなら2次微分を用いる最適化手法ニュートン法とかでもいいのではとも考えられます。 ですが論文では Second order methods have been previously used for DNN training … However achieving good convergence results on large scale DNN training problems like ImageNet classification has been difficult.（2次を用いたDNN学習は以前からあった … しかしImageNetを分類するような大規模なDNNの学習で良好な収束結果を達成することは困難だった。） と書いてありました。 対してK-FAC（https://medium.com/@osawa1021/k-fac%E3%81%A8%E3%81%AF-de30537f7096）のような最近の自然勾配に基づく方法やNeumannべき級数を使った方法（Krishnan et al 2017）の方がImageNet分類のような大規模な問題をうまく訓練することができるらしいです。

技術や手法のキモはどこ？

以下の２つが挙げられます。

・分散深層学習: Data Parallel

・非線形共役勾配法を用いたDNN

恐らく重要なのは後者ですが論文に書いてあった分散深層学習についても書きます。

分散深層学習 : Data Parallel

「分散深層学習」にはData ParallelとModel Parallelという2通りのアプローチがあることが知られています。

図1　分散深層学習（https://research.preferred.jp/2018/12/model-parallelism-in-dnn/より引用）

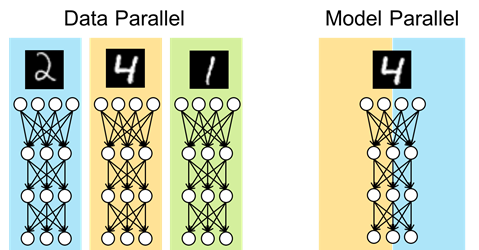
Data Parallelは、全プロセスに同じモデルのコピーをして訓練することでバッチサイズをプロセス数倍し、学習を高速化させる手法です。

深層学習を以下の図のように簡略化して描くとするなら

図2　深層学習の簡略図（https://www.slideshare.net/WeeHyongTok/distributed-dnn-training-infrastructure-challenges-and-lessons-learned?qid=8cc17052-6090-4574-ba3f-21ed1759f3a1&v=&b=&from_search=10より引用）

分散深層学習 : Data Parallelは以下のように描けます。

図3　分散深層学習 : Data Parallelの簡略図（https://www.slideshare.net/WeeHyongTok/distributed-dnn-training-infrastructure-challenges-and-lessons-learned?qid=8cc17052-6090-4574-ba3f-21ed1759f3a1&v=&b=&from_search=10より引用）

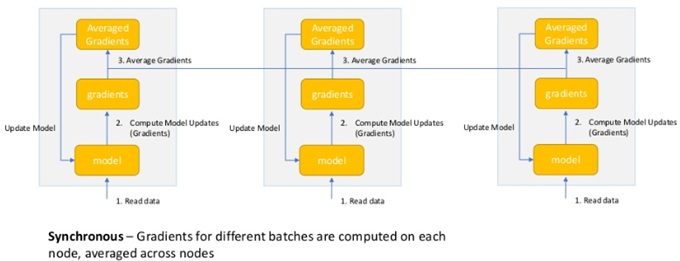
これにより1024GPU上でImageNetによるResNet-50の学習を15分で行うなどの実績を上げています。このような複数プロセス、複数ノードを用いた分散深層学習によってニューラルネットの訓練は高速に行えるようになっており、分散深層学習は現在の深層学習の基盤を支えているといえます。

より詳しく知るなら論文を読むことをおすすめします。

論文中に出てくるWorkers, Seversって何だ？となりますが、説明は以下の図のようになります。

図4　WorkersとSevers（https://www.slideshare.net/WeeHyongTok/distributed-dnn-training-infrastructure-challenges-and-lessons-learned?qid=8cc17052-6090-4574-ba3f-21ed1759f3a1&v=&b=&from_search=10より引用）

非線形共役勾配法を用いたDNN

非線形共役勾配法のアルゴリズムは以下のようになります。

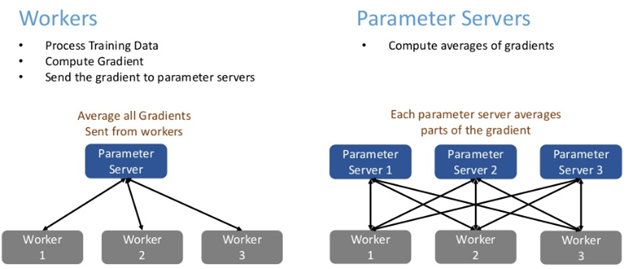
Calculate Preconditioner（Preconditionerを計算する）とは一体何でしょうか。

まずはここについて見ていきます。

（１）Quasi Newton Pre-conditioner

非線形共役勾配法はヘッセ逆行列を求める必要があるため、これを最適化する必要があります。

～ 補足 ～ 古い記事になってしまいますがhttp://www.orsj.or.jp/archive2/or59-03/or59_3_131.pdfでは ” 目的関数のヘッセ行列やその近似行列を利用する必要があるため、記憶容量や計算量の関係で，問題に対して直接適用することができないことがある” という問題が挙げられているためヘッセ（逆）行列を求めるのは処理的に重いことが分かります（実際どうなのかは分かりませんが…）。

そこでヘッセ行列を準ニュートン法で用いられるBFGSという更新方法に着目しています。

BFGS法によるヘッセ行列の近似は以下の式で表される。ヘッセ行列の対角成分を求めるという制限をかけることで処理を軽くしているようです（通常は対角成分だけではない）。過去の勾配との差を取れさえすれば良いのがキモらしいです。

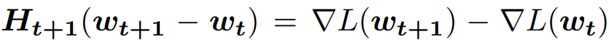
これにより処理が軽くなったとのことです（メモリ上で計算する必要がなくなった）。

以上を用いた処理(Quasi Newton)Pre-conditionerのアルゴリズムは以下です。

分かりづらかった場合は準ニュートン法で調べると分かるかもしれません。

（２）Online Stochastic Line Search

次に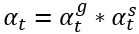について見ていきます。

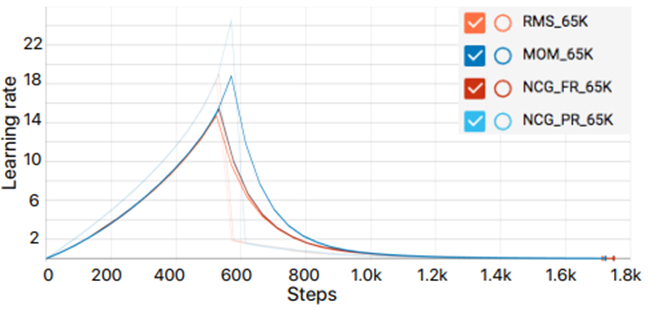
はglobal step lengthと呼ばれるもので以下の図のようなふるまいをします。

図5　αt^g（global step length）のふるまい

次にについてです。は1.0で初期化されています。

Loss関数がある一定の割合（論文では2%）以上増加したらの値を2.5%減少させます。

一方でLoss関数が減少もしくは変化がない（論文ではLoss関数の増加量が1%未満）ならを2.5%増加させます（最大で1.0になるまで）。

閾値1%、2%、2.5%はLoss関数の分散に依存するハイパーパラメータであるのでより良い性能のために調整することも良いと思われます。

どうやって有効だと検証した？

非線形共役勾配法を使って「Resnet-50モデルを用いたImageNet画像分類」と「Resnet-32モデルを用いたCIFAR-100画像分類」を行っています。

ここでは「Resnet-50モデルを用いたImageNet画像分類」の結果だけ見ていきます。

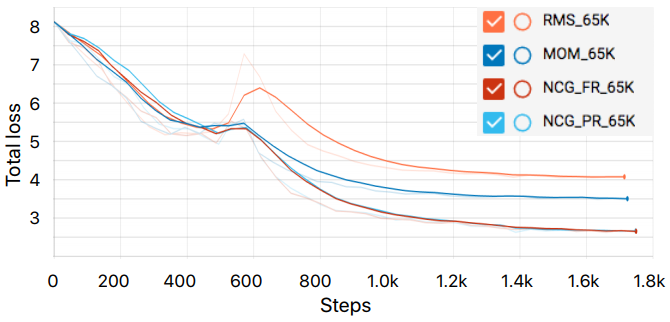
以下の図6は「Resnet-50モデルを用いたImageNet画像分類」によるLoss関数です。

・RMS_65K ( RMSProp )

・MOM_65K ( SGD with momentum )

・NCG_FR_65K ( 非線形共役勾配法( FletcherReaves ) )

・NCG_PR_65K ( 非線形共役勾配法( PolakRibiere ) )

の4つのoptimizerを用いて比較しています。

図6　「Resnet-50モデルを用いたImageNet画像分類」によるLoss関数

処理に必要な実測時間( Wall time( hours ) )は以下の図7のようになります。

図8　「Resnet-50モデルを用いたImageNet画像分類」によるWall Time

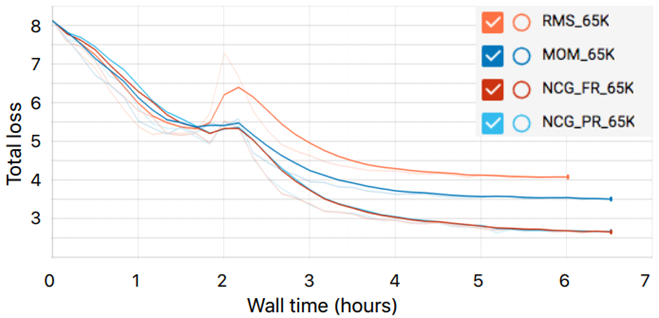
どちらにおいても非線形共役勾配法の収束性が優れていることが分かります。

次に以下の図は「Resnet-50モデルを用いたImageNet画像分類」でさまざまなoptimizerを使用して学習されたResnet50モデルのトップ1のテスト精度を示しています。そしてmini-batchサイズを512から98304に変化させたときのグラフです（epoch数は90）。

図9　「Resnet-50モデルを用いたImageNet画像分類」でさまざまなoptimizerを使用して学習されたResnet50モデルのトップ1のテスト精度

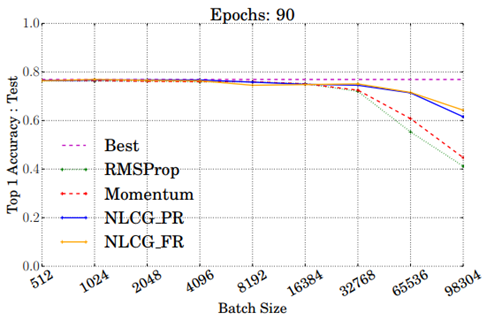
さらにbatchサイズ65536のときに注目してepoch数を変化させてみると以下の図のようになります。

図10　 batchサイズ65536のときに注目してepoch数を変化させる

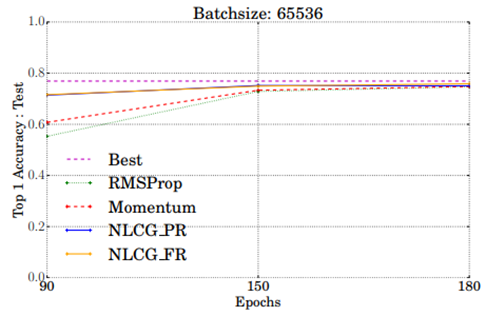
batchサイズ98304のときに注目してepoch数を変化させてみると以下の図のようになります。

図11　 batchサイズ98304のときに注目してepoch数を変化させる

議論はある？

大規模なミニバッチを使用した学習は分散深層学習をスケールアップするのに必要不可欠となります。

この論文ではNLCG optimizer（非線形共役勾配法）が共役勾配とPre-conditionerを使用して既存の方法より学習の収束速度を向上できたことを実証しました。

この研究では主に大規模なミニバッチにフォーカスを当てていました。

そのため勾配は分散が小さく、Pre-conditionerと共役探索方向の計算が意味のあるものになり、安定します。

ですがミニバッチが非常に小さくなると（例えば128）、勾配の分散が増大し、NLCG法が不安定になります。 

そのためより小さなミニバッチ、高勾配分散に対して安定したNLCG法を考える必要があります。

次に読むべき論文は？

未定。